
長野県長野市立若槻小学校5年1組の担任で、この日の授業者である宮澤幸一先生より、授業(「正方形を4つの合同な図形に分けよう」)の総評や、算数の指導上留意されている点について伺いました。また、同校学校長、清沢喜代登先生に「子どもたちの学び舎である『学校』にとって大切なものとは何か」をテーマにお話しいただきました。併せてご覧ください。
をご参考ください。
授業を終えて
西山氏
本日はお疲れ様でした。これからおもしろくなりそうだ、というところで授業が終わってしまったような…。
宮澤先生
ようやく子どもたちの中に見えてきたかな、という感じのところで終わってしまいましたが…。実は授業当日の朝まで迷っていたんです、ここ(対角線を回転させる)まで要求するべきかどうか…。
西山氏
本時の指導案では(四角形の)対角線の回転までになっていましたが、子どもたちの理解度は予想通りという感じでしたでしょうか。
宮澤先生

授業展開については、朝まで迷っていました。ここまで要求するべきか。クラスの子たちは、(対角線の回転の)前の段階、(折り紙を)半分にして、それをまた半分にすると合同な図形が4つ出来るというところまでで、充分楽しめるのではないかな、と。でも実際に授業をやってみたら、(折り紙を)半分にして、その後斜め半分に折るというところが意外と出てこなかったんですね。提示の仕方にも少し問題があったのかな、と思いました。ですから、ひとりの男の子が対角線を回転するような考え方をやっていたので、これをクラスでぶつけてみようかな、と考えました。最初に提示した正方形4つの折り紙の隣に、直角二等辺三角形が4つになる折り紙をひし形のように置いてみたら、四角形の対角線が回るというか、正方形と対角線の位置が動いているぞ、ということを匂わせてみました。
子どもたちに何か考えさせたいと思うときには、こちら(教師)が仕掛けをするべきなんですよね。ただなんとなく題材(教材)を出しておいて、気づいた何人かの子どもたちだけで「その考えはいいね」と進めていくのではなく、そのような見方をしてほしいのであれば、授業の中で先生の発問の仕方、提示の仕方、意見の取り上げ方もあるのですが、そういうところで子どもたちの考える視点をそれとなく誘導していきたいなと思っています。
今日の授業でも、正方形が4つ出来るときの対角線の十字が、(回転して)直角二等辺三角形が4つになるまでの途中にも(合同な図形が)存在しないかな、と考えたと言う子がいたんですね。対角線を回転させたい、この対角線が回っているのが見えた!とね。
西山氏
授業の後に、その考えを発表していた子が「扇風機を見て思いついたんだ!」と言っていましたね。
宮澤先生
そうでしたね。
西山氏
授業の最後は、関心のある子がどんどん黒板の前に出てきて話し合いが始まり盛り上がっていたのですが、こういうことは日常的によくあることなんでしょうか。
宮澤先生
今日の授業の中でも、一番後ろの子がみんなに説明する場面がありましたが、ちゃんと説明をしたいときは、前に出てきてみんなに向かって言わないと伝わらないんじゃないかな、ということは言っていますね。
あとは、小さくて見えなかったら前に出てきて見てもいいよ、というようなことも伝えています。
自ら手を伸ばす習慣を
宮澤先生

何事においても、自分から動く、です。
(しつけの一環として)手を後ろにおいて、机の上に○○を出しましょう、次に○○を使いましょう、ということではなくて、自分で問題解決をするためにこれが欲しい、あれが必要だと動けるように、自分から欲しいものを要求できるようにということは、意識して育てていこうと思っています。
今日黒板まで出てきた子というのは、自分で(黒板の折り紙を)見たかったんですよね。近くに来て、対角線がどう動いているのか、確認したかったんでしょうね。
今クラスは、運動会の前なので赤チームと白チームで分けて机を並べています。クラスの真ん中に大きな作業机を置いて遮っている感じです。クラスの中で「チーム」という意識があって、チームの中で話し合うことは自然に出来ています。でもひとりで考えないといけないときもありますからね。何か行き詰ったとき、停滞していたときなどは、「チームで相談して」と言うこともあります。「自分の意見を書けた人!」と質問をして、手を挙げた子がいますよね。「その人のところへ行けばきっとアイデア(ヒント)があるよ。自分から動いてみよう」と伝えます。これも自分で行きたいところへいってヒントを貰う。自分から動くというのは、日頃やっています。
中学年、高学年になるとどうしても子どもが受身的になりがちなんですね。考え方はいいから答えを早く教えてくれ、早く解き方を教えてほしい、という子も出てきます。もっと言えば、塾で習っているから算数はいい、という気持ちになってしまう子もいますよ。算数は、答えまでの途中が面白いんですよね。答えはひとつしかないけど、その道筋は自分では思いも付かなかったという発見があったりね。今日授業中にでた「扇風機」なんていう発想を聞くと「あぁ~!」と納得する子もいるわけですからね。教室はそういうことを共有できる場でありたいと思います。
塾で勉強している子は、お金をかけて時間をかけて自分で力をつけたいと思って勉強をしているのでそれはそれで立派なことです。でも、その途中にある考え方や、自分がどう考えるか、この問題を解くにはどの道具を使えばいいのかな、よし、これを試してみよう、ということを選択できる機会を多く提供するようにしています。それが「使える力」になると思うんですよね。
教材研究にアイテムを使う
西山氏
アイテムからヒントを得て、今日この教材を選ばれたとのことですが…
宮澤先生
アイテムの中では正三角形を題材(左:資料①)にしていましたが、四角形の方がへそ(対角線の交点)が分かりやすいと思いました。正三角形の重心や中心の存在を見破るのはちょっと難しいかな、と感じたので。二等辺三角形が見えてくるといえば見えますが、アイテムの解答としてはそこまで要求していないんですね。対角線の交点を見つけるということは解説でも触れていなかったですしね。
「合同な図形」の単元内でどこまで習うのか、ということなんですが、私は、対角線の交点を中心にしてずらしていく(回転していく)ことの面白さを子どもたちに体験させたいな、と考えました。そのためには正方形の辺の対角線の交点を軸にして回転させていくやり方の方が、見やすいし入りやすいと考えました。それに、(ひとつのものの)半分のまた半分、四半分という考え方も、新学習指導要領では2年生の分数で扱いますから、子どもたちにとって自然なのかなと考えました。
今日の授業の中で、正方形の対角線を交点(中心)で回転さるという見方は子どもにさせたいのですが、そうしたことで出来る図形は、いつも合同であるということについての論証については深く扱わないようにしよう、と思いました。まだ四角形の合同条件は扱っていないので、ここで出来てくる四角形は、(正方形やひし形、平行四辺形でない)一般四角形ですので、それがいつでも合同といえる、ということを論証するのはかなり難しいことです。なので、折り紙を切って出来た図形を重ねたら同じだったという説明くらいで留めたいなと思いました。正方形のそれぞれの対角線を回転させてみたら、どこでストップさせてはさみで切って重ねてみても、みんな同じになるんだね、面白いね!というところを授業の中心にしたいな、と思いました。
西山氏
今回のようにアイテムの中のから問題をピックアップしたり、アレンジして展開したりというのはあることなんですか?
宮澤先生
学期に一回くらいでしょうか。
この前は「四角形」の単元から、ひし形の作図の問題(左:資料②参照)が面白くて取り上げました。私のクラスでは、アイテムの中の「発展させよう」の問題はやってもやらなくても自由だよ、というページにしています。出来たら凄いね!と褒めます。普通の小学生は出来なくても全然おかしくない問題です、と伝えています(笑)いい問題だけど難しい問題が入っているから、やれそうな人はチャレンジしてみてね、と。基本的には自由に、進みたい人はどんどん進んでやってもいいよと。単元テストがあるときには、日にちを決めて、この日までに○ページまではやってきましょう、と。まずはこどもが先行して、宿題としてはあとから私の方で「ここまで全員終わらせよう」と制限をかけていくやり方で進めています。私のいうペースで進んでいく子もいますし、すでに(9月初旬の段階で)半分以上終わってしまっている子もいます。アイテムの中の三角形の問題が終わっていた子もひとり、ふたりいたんです。でも今日の問題と結びついてはいなかったですね、きっと。
図形の問題は見方を少し変えた途端に、今まで見えなかったものが浮かび上がってくる驚きがありますよね。そういう経験を多くさせたいな、と思っています。
学校の取り組みとして
西山氏
連学年で単元を構成していくという考え方は清沢校長から伺いましたが、具体的に現場ではどのような事をされていきたのでしょうか。
宮澤先生

校長先生から説明があったと思いますが、本校では3年前から「関心・意欲・態度」をとにかく高めたいと考えました。ですので、そういう授業作りを目指す中で連学年算数が提案されました。教材研究の時間を先生たちで勤務時間の中に設けて、算数の話が勤務時間内に出来る環境をつくりました。算数を通して「関心・意欲・態度」を上げるぞ!と3年間信じて頑張ってきましたし、事実上がったと思います。
まず最初にした事は、先生たちの悩みを出し合うことでした。例えば中学年ですと、4年を担当する先生の中には去年3年を担当していた先生が多くいるんです。(長野市の場合は少なくとも2学年持ち上げで担任をするケースが大半です。クラス編成も2年で変わりますから。)4年生の先生というのは3年生の先生の気持ちがよく分かるんですよね。3年の先生たちが算数指導においての悩みを出すと、「そうそう!その単元は去年も出来なくてね…教科書どおりやっても駄目なのよね」「最初から条件を子どもたちに全部見せちゃうからなんじゃない」のようなヒントやアイデアを出してくれるんですよね。それだけでも大分違いましたね。単元配列なども、「1学期の最後にこの単元をやると駆け足になってしまうから、早めに入った方がいいよ」とアドバイスが出たり。そのような点でとても有効だったと思います。学年会でも同じ事をやれればいいのですが、学年行事などがあるとなかなか話が及ばないんです。出来れば同じような事を1年から6年まで通して出来ればいいんですけどね。中学に行くまでにこの力だけはつけておいて欲しい、そのためには低学年からこういうことに取り組んで欲しい、ということもあるでしょうしね。こういう話がどんどん出来るようになればもっといいなと思います。学校の組織というよりも研究会・研修会という形で縦に見通していける学習が出来ればいいですよね。
アイテムの有効活用
西山氏
算数指導において、学校の方針とどのような部分でこのアイテムが合致したのでしょうか。
宮澤先生
他校でもよく言われることだと思いますが、問題数が多いですよね。子どもたちが自分で読んでも分かる基本的な説明から、スーパー小学生級の難しい問題までたくさん入っているということ。1年間の学習内容が1冊になっているというものは、小学校の場合なかなかないんですよね。多くは学期制や前期・後期制のものなので。1年間の学習内容を見通すという点では、1冊になっている方が良かったんです。少し分厚くはあるんですが、それでも3学期分と考えれば決してそれ程大変な量ではないですね。そしてお値段もお手ごろというよりも安いくらいですよね。
子どもたちも、学習内容を振り返るときに見やすいと思うんですね。例えば2学期になって1学期の学習を振り返るとき、1冊だとすぐに振り返って思い出せるところがいいですよ。先生たちもね。
振り返るときというのは、単元同士の繋がりを考えるときに、子どもたちに「これはどこかでやったよね」と尋ねることがあります。そうすると子どもたちからは、自分のノートをめくって振り返ったり、アイテムを振り返ったりしています。そして「○月○日にやってる!」「アイテムの○ページにあった!」という声があがりますね。これは先ほどお話した、道具を自分で選ぶことと同じように、自分で振り返れるようにしたいと思っています。
私のクラスで言えば、アイテムの「発展させよう」の問題も、半数の子どもは挑戦しています。
中には赤ペンで、解答解説を見て写している子どもも何人かはいますけれどね。結構意欲的に関わろうとしています。自分でどんどん先のページ(未履修単元)に進んでしまって、分からない問題に当たるとどんどん赤で答えを書き込んでしまう子どももいますので、分からないところは慌てなくていいから、学校で勉強した後にまたやればいいんだよ、ということで、アイテムの表紙に「『発展させよう』は無理にやらなくてもいい」と書かせています。
最初から、答え(解答・解説集)も一緒に子どもに持たせています。自学自習が自分のペースで出来るようにですね。だからやろうと思えば、自分で答えを写してどんどん先に進めてしまうんですが、それは自分のためにならないですから、そういうことはさせたくないなという思いがあり、戒めの意味もあって表紙に書かせてあるんですが(笑)
西山氏
自習、宿題はアイテム中心ですか?
宮澤先生
そうですね。プリントもありますが。少人数指導も加配があって出来る学校ですので、その中でも取り組んでいます。
今の5年生で言えば、教科書のもっと奥にあるものを見たいな、もっと面白いことが隠れているんじゃないのかな、という好奇心は子どもたちの中にあると思います。アイテムの中には、ひとつの単元でも色々工夫された問題が入っているので、そういう見方、考え方も出来るんだな、ここは他の単元と繋がっていたんだなという面白さは、普通の問題集にはないものだと思っています。
他学年の先生にもアイテムはその都度紹介はしていますが、学年全体でというところまではまだ踏み切れないです。でも学校全体で見て、算数の力というのは上がってきています。NRTの結果も上がってきていますしね。全国学力調査テストの結果でも多少いいほうじゃないですかね。あまり詳しいことは他言できないんですが(笑)
昨年、筑波大学附属小学校(算数研究部)の細水先生に本校に来ていただいて授業をしていただいたことも影響していると思います。先生方の授業観、授業に対する姿勢も変わってきているんじゃないかと感じています。
西山氏
具体的にはどのような変化が?
宮澤先生
今まではドリルを繰り返してやることが中心でしたね。先生たちは本来まじめなので、出来ない子どもをなんとか出来るようにしたいというのが一番にあるんですね。例え20人できていても、3人できていない子がいれば、その3人をなんとかしなくてはいけない、と思う。その底上げを一生懸命やるんです。それこそ手取り足取り、ひたすら出来るようになるまでやる。そういう授業観がありました。ですからドリル的なもの、習得型の授業が多めになっていたのですが、活用力を育てるような問題を扱う授業が増えてきました。授業はバランスが大切なんですよ、と伝えています。先生たちが授業の中で、バランスを考えた構成をしてきているんじゃないかなと思います。
*取材にご協力をいただきました長野市立若槻小学校様には、心より感謝御礼を申し上げます。
*本記事は、学校様のご了解をいただいた上で掲載いたしております。外部転載等につきましては固くお断り申し上げます。
子どもたちは、「正方形を直線で切って4つの合同な図形に分ける」という問題にチャレンジします。果たして、どんな図形が出てくるのか。


子どもたちは、配られた折り紙を、切ったり、折ったりしながら図形を探していきます。その表情は真剣そのものでした。

授業の中ではグループで話し合う場面も。関心のある子は、どんどん黒板の前に出てきて、そこでも話し合いが始まります。

子どもたちが発見した合同な図形を黒板に貼っていくと…



ある「四角形」が貼り出されると「ん?」「なに?」と子どもたちは戸惑いの様子に。対角線を交点で回転させたときに出来る四角形(下図参照)に注目した子どもが出てきました。


すかさず、宮澤教諭は「何かひらめいた人?」と、子どもの着目点をクラスの中に広げていきます。
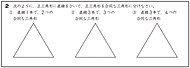
【資料①】
新版「アイテム」算数 5年 「合同な図形」(チャレンジしよう)より
*本時で参考とした現行の「アイテム」の問題は日本教育新聞・企画特集にて掲載。(クリックで拡大)

【資料②】
「アイテム」算数 5年 「四角形」(発展させよう)より
*同問題は、新版「アイテム」算数4年「四角形」(チャレンジしよう)にも掲載。(クリックで拡大)





